PROFESSORA JESSICA MATEMÁTICA

CALCULANDO O COFATOR DE UMA MATRIZ

O cofator auxilia no cálculo de determinantes de ordem maior que três, em razão de ser utilizado no teorema de Laplace, uma vez que este é usado justamente para o cálculo de matrizes quadradas de ordem n.

Cada elemento da matriz possui o seu cofator, e temos a expressão que determina o cálculo deste cofator. O cofator de a_ij é o número A_ij em que:

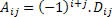
Você deve estar se perguntando o que é este D_ij. Temos que D_ij é o determinante da matriz que é obtida através da matriz A, contudo a i-ésima linha e j-ésima coluna são eliminadas.

Este conceito só será compreendido quando o aplicarmos.

Exemplo: Determine os cofatores dos elementos: a₁₃ e a₂₂, da matriz A.

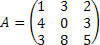
Como vimos, para calcular o cofator do elemento a₁₃ iremos utilizar a expressão que conhecemos do cofator.

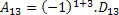
Note que precisamos determinar a matriz D₁₃ para calcular o seu determinante. Esta matriz será obtida eliminando a linha 1 e a coluna 3 referente à matriz A. Sendo assim, temos que:

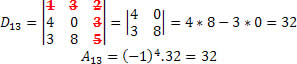
De forma análoga, procederemos para encontrar o cofator do elemento a₂₂.

Pelo teorema de Laplace podemos relacionar os cofatores de uma matriz para determinar o determinante de uma matriz com ordem n

REGRA DE CHIÓ (matrizes)

No perpassar dos conceitos de determinantes, aprendemos formas e procedimentos que ajudam a encontrar os determinantes das matrizes quadradas de ordem 3. A regra de Chió nos permite calcular o determinante de uma matriz de ordem n, utilizando uma matriz de ordem menor (ordem n-1).

Entretanto, para se utilizar esta regra é necessário que o elemento a₁₁ seja igual a 1. Caso isso ocorra, poderemos utilizar os passos desta regra. Veja:

• Suprima a primeira linha e a primeira coluna da matriz.

• Dos elementos que restaram, subtraia o produto dos dois elementos suprimidos (um da linha e o outro da coluna) correspondente a este elemento restante. Por exemplo, no elemento a₂₃ você realizará o produto do elemento da segunda linha da coluna que foi suprimida pelo elemento da terceira coluna da linha que foi suprimida.
• Com os resultados das subtrações realizadas no passo anterior, será obtida uma nova matriz, matriz esta com ordem menor, entretanto com determinante igual à matriz original.

Veja no exemplo a seguir.

Matriz com elementos em destaque

De cada elemento da nova matriz subtrairemos o produto dos elementos suprimidos (elementos coloridos).

Obtendo uma nova matriz aplicando a regra de Chió

Veja que o cálculo do determinante desta nova matriz pode ser feito pela regra de Sarrus. Determinante este que será o mesmo da matriz inicial de ordem 4.

Mas lembre-se que esta regra só pode ser utilizada se o elemento a₁₁ for igual a 1, caso contrário não será possível suprimir os elementos da linha e da coluna.

matrizes(adição e subtração)

A operação com qualquer matriz sempre resultará em outra matriz, independentemente da operação utilizada.

Antes de falarmos da adição e da subtração de matrizes, iremos relembrar do que uma matriz é formada: toda matriz tem seus elementos que são dispostos em linhas e colunas.

A quantidade de linhas e colunas deve ser maior ou igual a 1. Cada elemento vem representado com a linha e a coluna que pertence. Exemplo: Dada uma matriz B de ordem 2 x 3 o elemento que se encontra na 1º linha e 2° coluna será representado por b₁₂.

►Adição

As matrizes envolvidas na adição devem ser da mesma ordem. E o resultado dessa soma será também outra matriz com a mesma ordem.

Assim podemos concluir que:

Se somarmos a matriz A com a matriz B de mesma ordem, A + B = C, teremos como resultado outra matriz C de mesma ordem e para formar os elementos de C somaremos os elementos correspondentes de A e B, assim: a₁₁ + b₁₁ = c₁₁.

Exemplos:
Dada a matriz A=

3 x 3 e matriz B=

3 x 3, se somarmos a A + B, teremos:

3 x 3

Observe os elementos em destaques:

a₁₃ = - 1 e b₁₃ = - 5 ao somarmos esses elementos chegaremos a um terceiro que é o
c₁₃ = -6. Pois -1 + (-5) = -1 – 5 = - 6

O mesmo ocorre com os outros elementos, para chegarmos ao elemento c₃₂, tivemos que somar a₃₂ + b₃₂. Pois, 3 + (-5) = 3 – 5 = - 2

Assim: A + B = C, onde C tem a mesma ordem de A e B.

►Subtração

As duas matrizes envolvidas na subtração devem ser da mesma ordem. E a diferença delas deverá dar como resposta outra matriz, mas de mesma ordem.

Assim temos:
Se subtrairmos a matriz A da matriz B de mesma ordem, A – B = C, obteremos outra matriz C de mesma ordem. E para formarmos os elementos de C, subtrairemos os elementos de A com os elementos correspondentes de B, assim:a₂₁ – b₂₁ = c₂₁.

Exemplos:

Dada a matriz A =

3 x 3 e B =

3 x 3, se subtrairmos A – B, teremos:

3 x 3

Observe os elementos destacados:

Quando subtraímos a₁₃ – b₁₃ = c_13, -1 – (-5) = -1 + 5 = 4

Quando subtraímos a₃₁ – b₃₁ = c_31, - 4 – (-1) = -4 + 1 = -3

Assim A – B = C, onde C é uma matriz de mesma ordem de A e B